It would be helpful to have a flow chart of which tactics to use in which situations, in order to solve a differential equation. I intend to make one, and want it to look sort of like this flowchart to tell if an infinite series converges.

Some previous attempts like this one have been done, but they are not as complete because they do not explain the idea behind each tactic, and do not include very many methods to solve a differential equation. Many other previous charts only work for linear, or 2nd order equations. This chart should work for any differential equation, or at least recommend that a numerical method is used to approximate it.

To make this chart, we need a list of ways to solve differential equations, and when to use them. Below is a chart

Tactics to Solve an Ordinary Differential Equation, and When To Use Them

Variation of Constants (aka Variation of Parameters)
Integrating Factor
Euler’s Guess, or other guessing based on the form of f(t)
Separation of Variables
Numerical Methods (Euler’s, Runge Kutta, Multi-Step Methods, Multi-Derivative Methods, Exponentially Weighted Moving Average, etc)
Method of Undetermined Coefficients. Used to find a Particular solution
Power Series
Laplace transform

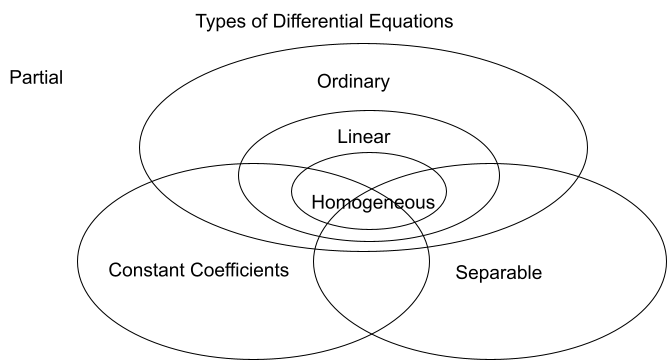
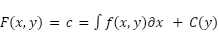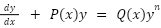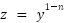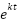Tactic	Type of Solution	Method Requirements:	How it works
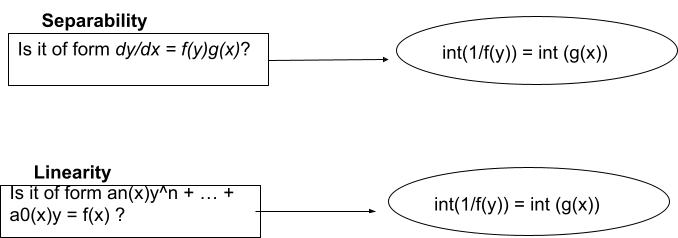
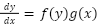
Separation of Variables	General	1st order, of form:	With only 2 variables, get each variable on opposite sides of the equation, and integrate to solve them.
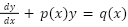
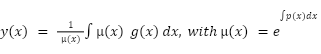
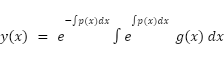
Integrating Factor	General	1st order. Linear (of this form): BTW, the general solution to a 1st order linear DE is: As a result There is no guarantee that the integrals are solvable. If you want, you can just plug the equation into the formula above, and save yourself a lot of effort.	This is using the “product rule” (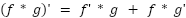) in reverse. 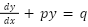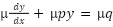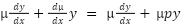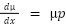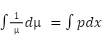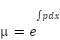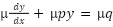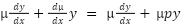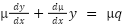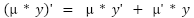You multiply each side of the differential equation by a function μ(x) get this into the product-rule form: by finding the function μ(x) such that: so , and this is separable (p is function of x) And now you can use product rule property 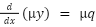, and this is almost separable (we can still solve it by separation of variables) 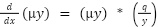, and this is separable (q and y are functions of x
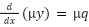
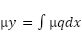
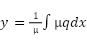
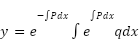
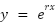
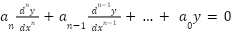
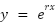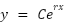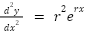
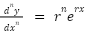
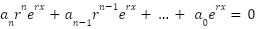
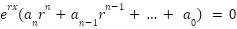
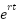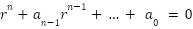
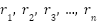
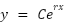
Euler’s Guess	General	Linear, Homogeneous, constant coefficients (of this form):	You know the solution must take the form: (or ), and so … is never 0 for any r and t Solve for the roots r of this polynomial, to find every solution If a root is real, then that root’s solution is written^[a] as: If a root is repeated “k” times, then that solution can also be written as 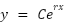, BUT there are “k” solutions. The other “k-1” solutions can be found using the technique of reduction of orders. So all “k” of these solutions can be found. 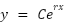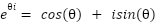If a root is imaginary, , then the solution can be written as a sinusoid, using Euler’s identity: The sum of these imaginary roots can be rearranged, and can produce real solutions. 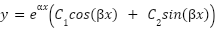This can be written in the form: *Note that there MUST be an even amount of imaginary solutions. So the imaginary solutions can always be grouped together to form a sinusoidal real solution To find the general solution, just add all the forms of the solutions found
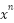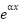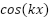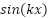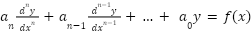
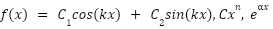
Undetermined Coefficients	Particular	Linear, constant coefficients, with forcing term being a polynomial in , exponential in , sinusoid of the form , and , or a product or sum of these functions, as long as the term is finite. or a linear combination or product of these functions	Assume that the solution takes a certain form. Then solve for the coefficients of this form by using the initial conditions, or plugging it back into the differential equation and solving for the^[b] coefficients
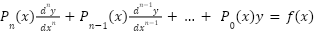
Cauchy Euler Equations	General	where 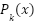is a polynomial of degree “k” or lower ??? Does it have to be homogenous^[c]??? f(x) = 0? for the guess to work? ??? Can Pk(x) be any polynomial, or does it HAVE to be for the form Pk(x) = x^m for the guess to work?	Use the guess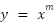
Variation of Parameters			Find the solution to the corresponding homogeneous equation (this is called the “complementary” equation), then find a particular solution. Add them together to find the general solution
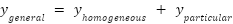
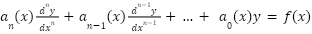
Power Series Form	General if you can evaluate the series. Otherwise approximate	Linear (of this form): where 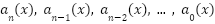must be analytic (can be written as a power series). The coefficient terms must be able to be represented as a polynomial (analytic), and cannot be of the form 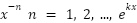, etc. . 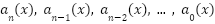terms must be analytic/finite near the approximation, and wherever the expansion is centered. The	Know that the form can be approximated exactly by an infinite power series, and then find constant terms of the series to find the series. If the equation is linear, then you can assume the solution can be written in the form: 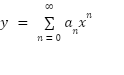, then derivatize this to find y’, y’’, y’’’, … and substitute them into the differential equation to solve for the coefficients. Once you know the coefficients, then you know y. Finding the coefficients may involve a recurrence relation.
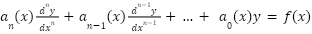
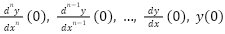
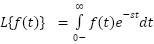
Laplace Transform	General	Linear (of this form): And initial conditions at x = 0 must be known	Switch to frequency domain, and all higher derivatives can be written in terms of a lower derivative and an initial condition. Then use a reverse-laplace transform to get back in the time domain. Usually you can look up the laplace transform of a function from a table of these.
Numerical Methods	Approximate, numerical solution (a set of points that are very close to the solution).	Usually, only works for any order. But some numerical methods can approximate solutions of other forms.	Use an initial condition, and knowledge about where the function is going, to predict/estimate where it will go in the future. A numerical method for solving an ODE can be: Multi-step: uses previous points to calculate future ones Multi-derivative: uses derivative of the DE before and after a point to calculate that point Some specific numerical methods include: Euler’s Runge-Kutta
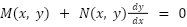
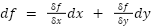
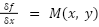
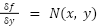
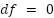
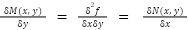
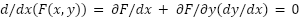
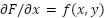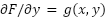
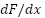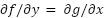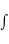
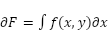
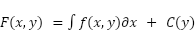
Exact Equations	General	Has form: which is the same as: where: The equation is exact if and only if:	Given that F(x,y)=c is a solution to a differential equation we can find the differential equation by applying chain rule to F. and To test thatis an exact first order differential equation, . Notice that the partials are still first order. After testing… Integrate with respect to x. Differentiate with respect to y. 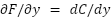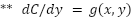3. Integrate ** with respect to y and solve for C. 4. Assemble your solution and there is no need to add the constant obtained by solving for C. ^[d]^[e] You can solve this using the integrating factor method

Tactics to turn a hard-to-solve differential equation into an Easy-To-Solve one

Reduction of Order
Z-Substitution. If a differential equation has the nonlinear form , we can substitute , and get a differential equation that is linear.
Adding general Solution to corresponding Homogeneous Equation to Particular Solution for the actual equation. So instead of finding the general solution to the nonhomogeneous, can find the general solution to the homogeneous, and a particular solution to the non-homogeneous (which “shifts” the homogeneous solution by a certain amount, so that it is the non-homogeneous solution). Only works for linear equations
Break a down a higher order DE into a system of lower order DE’s, find eigenvalues, eigenvectors, and eigenfunctions, and plug these into the known form of the solution

Tactics to tell if a differential equation has a solution

Picard’s theorem
others?

Tactics to tell if the differential equation has a solution, and if a solution is unique

Picard’s theorem
Lipschitz Condition.

How does a solution blow up?

A solution blows up at a discontinuity or if you obtain a complex solution. (need to double check).

Ways to classify a differential equation:

Order (highest derivative)
Differential vs Integro-Differential Equation (does it have integrals?)
Constant Coefficients
Separable
Ordinary vs Partial
Linear vs Nonlinear
Homogeneous vs InHomogeneous

What tactic can be used when:

Questions we still have:

When do numerical methods not work (Stiff equations, convergence, ...)?
When do Matrix methods work?
When can you break down a higher order ODE into a system of lower order ODE’s, and can this be done for nonlinear non homogeneous ODE’s?^[f]
When does Laplace Transform converge and work?
Interval of convergence, and formulas for error of approximation, for each of the methods above
Are there any ways to tell if a DE has a solution (besides Picard’s theorem)

[a]Be careful not to confuse this with Euler's Method, a numerical solution method. Also, this method works well for second order, but higher order requires factoring tricks that can be difficult.

[b]This method required knowing the homogeneous solution first.

[c]You will again separate the two cases, homogeneous and particular, and solve them separately.

[d]What about solving systems of ODE?

[e]I wasn't sure when you can break down a higher order ODE into a system of lower order ODE's. Doesn't it have to be linear in order to break down a higher order into a system of lower order ODE's?

[f]Can any higher order ODE be broken into lower order ODEs